Bueno, aunque se que el post no va a tener mucha acogida, lo subo básicamente por una razón.
No es simplemente vomitar teoría inútil que no sirve para nada, esto se utiliza para muchas cosas, incluso con el tiempo a mi me ha asombrado. Descubrí con el tiempo que esto también se utilizaba para el análisis de gráficas en el Trading para obtener predicciones en corto ya que son señales simétricas.
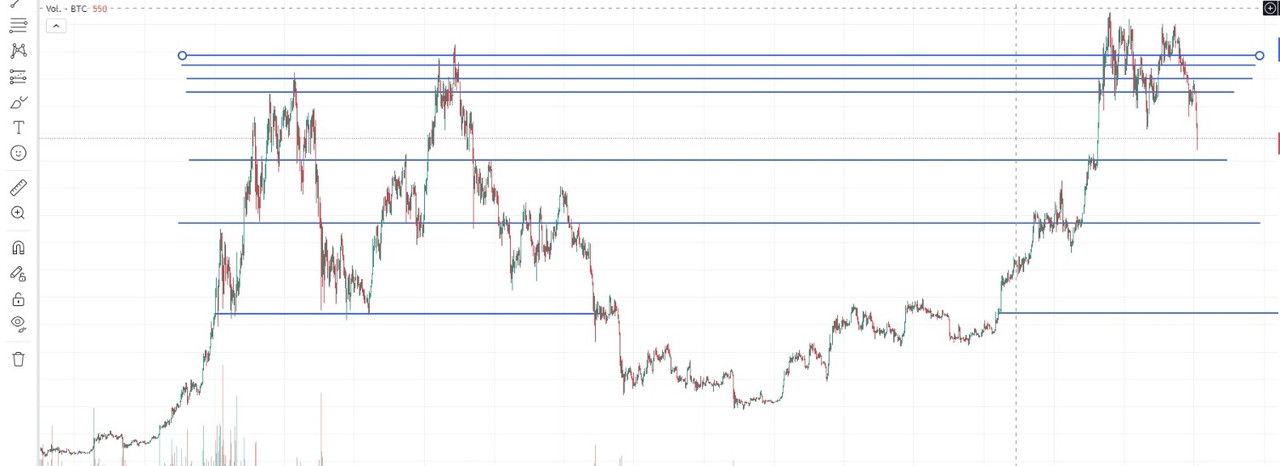
La ultima vez que lo he utilizado ha sido para ayudar a un colega que está en Moto3 para intentar buscar una frecuencia en la moto que la hacía entrar en resonancia en una curva de un circuito al pisar los pianos.
Ósea que es algo que se utiliza y bastante guapo de utilizar cuando lo entiendes. Da muchísima información, aunque en el foro lo voy a tirar por donde a mi me lo enseñaron, a las comunicaciones.
Lo voy a intentar explicar de la forma más sencilla posible, que no os acojonen ni os de pereza solo porque veáis que son nombres técnicos, creo que si lo leéis lo vais a entender.
Para entender esto, primero debemos hablar un poco sobre matemáticas y formas de representar datos. Normalmente, usamos el plano Espacio-Tiempo para representar señales. Sin embargo, para analizar y tratar estas señales, es más útil utilizar el plano de las frecuencias, también conocido como dominio de la frecuencia.
Imaginad que tenemos una señal de audio con la forma coseno (el más típico) y que este audio dura 10 segundos

Amplitud = coseno(t)
Donde “t” toma los valores de 1 a 10 en incrementos de 1 segundo
Coseno(0) = 1
Coseno(1) = 0,54
Coseno(2) = -0,41
.
.
.
Coseno(10) = -0,83
Si tomásemos valores de 1 a 10 la representación nos queda de esta manera:
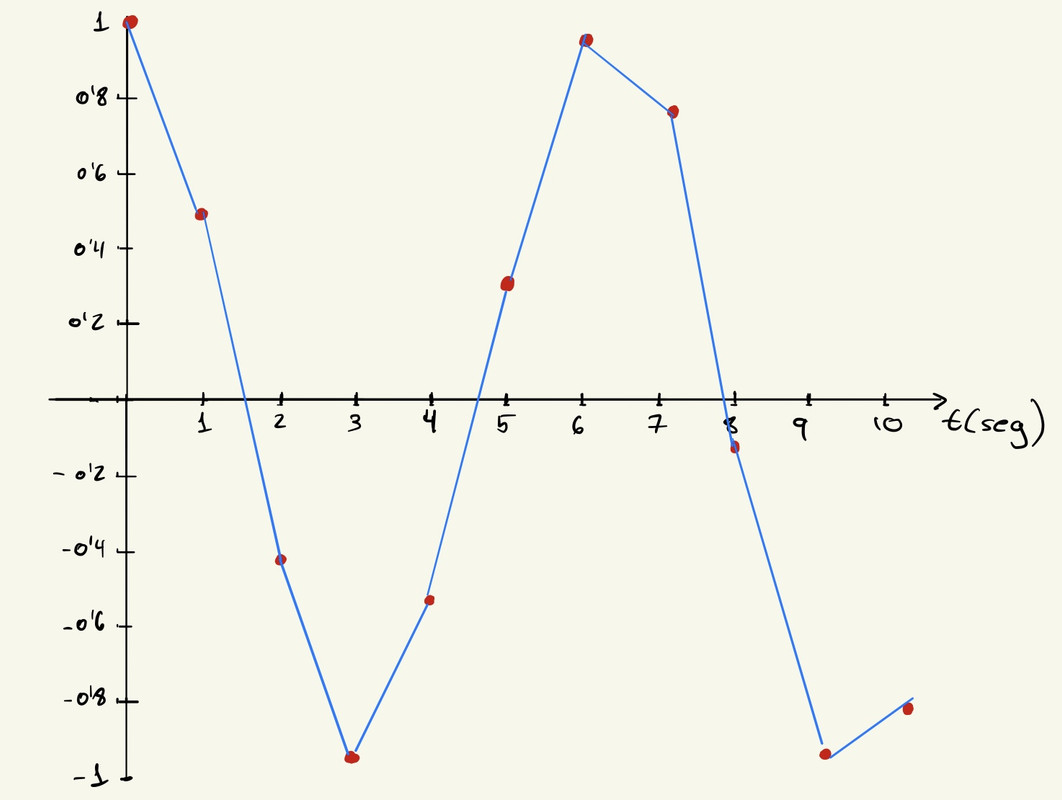
A la hora de unir los puntos y reconstruir la señal original, se pierde muchísima información (no es igual que la señal original) y escucharíamos cortes en la señal o no iríamos algunos instrumentos en la señal entre otras muchas cosas.
Ósea, para hacer una reconstrucción perfecta de la señal original tendríamos que enviar infinitos puntos y por tanto el archivo ocuparia muchísimos Gigas. Esto solo sería para una voz, imaginad si en el audio se introducen más elementos como instrumentos o efectos.
Cuando enviamos información o archivos por internet, interesa que estos paquetes de datos sean lo más pequeños posible y que con ellos obtengamos muchísima información para ocupar el menor ancho de banda posible. Imaginad una canalización de agua, la tubería es el ancho de banda y los paquetes/información es el agua. Está tubería es la que se comparte con todo el mundo
Como veis, trabajar en el dominio del tiempo es muy pesado. Por eso, a una persona se le ocurrió trabajar en el dominio de la frecuencia ya que el tiempo y la frecuencia están relacionados
Para pasar del dominio del tiempo al dominio de la frecuencia se utiliza la Transformada de Fourier que ya he medio explicado en otros Posts (Tampoco tiene mucho sentido explicarlo en el foro).
Al pasar esta señales del tiempo al dominio de la frecuencia obtenemos muy pocos puntos de representación. En el caso del coseno sería esta representación:

Es decir, 2 impulsos a diferencia de infinitos puntos como era el dominio del tiempo, estos dos impulsos son los que se envían.
Al realizar esta conversión del tiempo a la frecuencia obtenemos lo que se conoce como el espectro de la señal, en la que vemos las frecuencias más importantes de la señal y que frecuencias suenan.
Esto es lo que se llama el espectrograma de una señal, es decir, la representación en frecuencia de la señal. Aquí es donde se puede detectar que notas son las que suenan y con ello podrías sacar la partitura de un audio sin tener ni puta idea de música.
¿Que son las otras marcas?
Los instrumentos de cuerda, como el violín cuando las haces vibrar, su nota musical vibra a una frecuencia haciendo su ruido característico, pero hasta que la cuerda deja de vibrar emite otros sonidos a diferentes frecuencias que son los llamados Armónicos. Son estos Armónicos los que caracterizan un instrumento u otro. Hablo de instrumentos de música pero esto ocurre con todo: vibraciones de motores, voces…
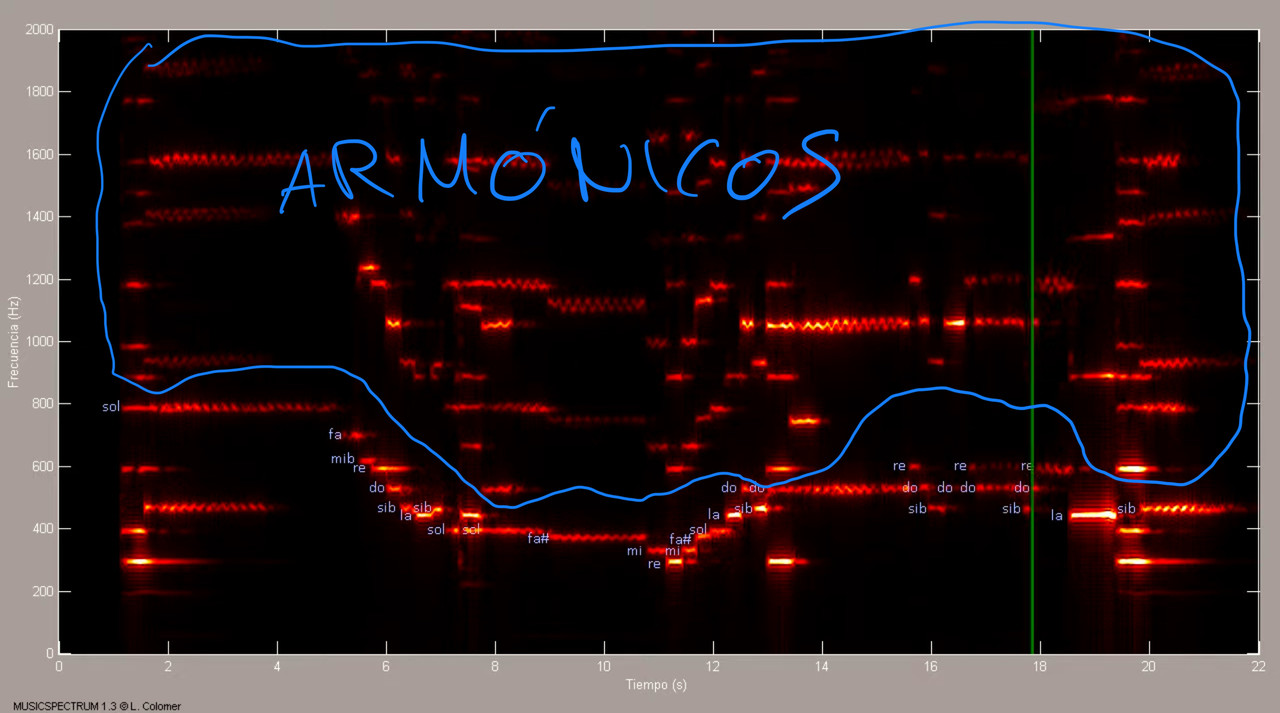
Una manera de reducir el tamaño sería quitar estos armónicos, ahorrando así en tamaño del archivo y de comprensión.
Es decir, si el audio tiene 40 sonidos y son necesarios 2 puntos para la reconstrucción de estos, tendremos que enviar 80 puntos en los paquetes de datos.
Pero si hemos calculado el espectro de la señal y observamos que únicamente para poder escucharlo necesitamos 10 sonidos ya que el resto son armónicos, necesitaremos enviar únicamente 20 puntos.
Conclusión, hemos pasado de 5 Gigas de audio a 10Kbytes
Matemáticamente lo que se hace es elevar al cuadrado, el espectro de la señal (frecuencia) tiene amplitudes a la mitad de la señal original (tiempo) por lo que al elevar al cuadrado, las amplitudes se hacen más pequeñas y desaparecen. Solo van a quedar aquellas componentes de la señal que más importantes son de la señal.
La densidad espectral lo que representa es una magnitud (dB) de cuanto de presente está esa frecuencia en la señal y si es muy importante o no para la recepción del audio, lo que vamos a escuchar.
Esto resalta las frecuencias más importantes y atenúa las menos significativas. La densidad espectral muestra cuánta energía hay en cada frecuencia y nos indica qué partes de la señal son más importantes para el audio.
No es simplemente vomitar teoría inútil que no sirve para nada, esto se utiliza para muchas cosas, incluso con el tiempo a mi me ha asombrado. Descubrí con el tiempo que esto también se utilizaba para el análisis de gráficas en el Trading para obtener predicciones en corto ya que son señales simétricas.

La ultima vez que lo he utilizado ha sido para ayudar a un colega que está en Moto3 para intentar buscar una frecuencia en la moto que la hacía entrar en resonancia en una curva de un circuito al pisar los pianos.
Ósea que es algo que se utiliza y bastante guapo de utilizar cuando lo entiendes. Da muchísima información, aunque en el foro lo voy a tirar por donde a mi me lo enseñaron, a las comunicaciones.
Lo voy a intentar explicar de la forma más sencilla posible, que no os acojonen ni os de pereza solo porque veáis que son nombres técnicos, creo que si lo leéis lo vais a entender.
¿Qué es el espectro de una señal?
Para entender esto, primero debemos hablar un poco sobre matemáticas y formas de representar datos. Normalmente, usamos el plano Espacio-Tiempo para representar señales. Sin embargo, para analizar y tratar estas señales, es más útil utilizar el plano de las frecuencias, también conocido como dominio de la frecuencia.
¿Porqué usamos el dominio el dominio de la frecuencia?
Imaginad que tenemos una señal de audio con la forma coseno (el más típico) y que este audio dura 10 segundos

Amplitud = coseno(t)
Donde “t” toma los valores de 1 a 10 en incrementos de 1 segundo
Coseno(0) = 1
Coseno(1) = 0,54
Coseno(2) = -0,41
.
.
.
Coseno(10) = -0,83
Si tomásemos valores de 1 a 10 la representación nos queda de esta manera:

A la hora de unir los puntos y reconstruir la señal original, se pierde muchísima información (no es igual que la señal original) y escucharíamos cortes en la señal o no iríamos algunos instrumentos en la señal entre otras muchas cosas.
Ósea, para hacer una reconstrucción perfecta de la señal original tendríamos que enviar infinitos puntos y por tanto el archivo ocuparia muchísimos Gigas. Esto solo sería para una voz, imaginad si en el audio se introducen más elementos como instrumentos o efectos.

Cuando enviamos información o archivos por internet, interesa que estos paquetes de datos sean lo más pequeños posible y que con ellos obtengamos muchísima información para ocupar el menor ancho de banda posible. Imaginad una canalización de agua, la tubería es el ancho de banda y los paquetes/información es el agua. Está tubería es la que se comparte con todo el mundo
Como veis, trabajar en el dominio del tiempo es muy pesado. Por eso, a una persona se le ocurrió trabajar en el dominio de la frecuencia ya que el tiempo y la frecuencia están relacionados
T= 1/f
Transformada de Fourier
Transformada de Fourier
Para pasar del dominio del tiempo al dominio de la frecuencia se utiliza la Transformada de Fourier que ya he medio explicado en otros Posts (Tampoco tiene mucho sentido explicarlo en el foro).
Al pasar esta señales del tiempo al dominio de la frecuencia obtenemos muy pocos puntos de representación. En el caso del coseno sería esta representación:

Es decir, 2 impulsos a diferencia de infinitos puntos como era el dominio del tiempo, estos dos impulsos son los que se envían.
Al realizar esta conversión del tiempo a la frecuencia obtenemos lo que se conoce como el espectro de la señal, en la que vemos las frecuencias más importantes de la señal y que frecuencias suenan.
Espectrograma
Esto es lo que se llama el espectrograma de una señal, es decir, la representación en frecuencia de la señal. Aquí es donde se puede detectar que notas son las que suenan y con ello podrías sacar la partitura de un audio sin tener ni puta idea de música.
¿Que son las otras marcas?
ARMÓNICOS
Los instrumentos de cuerda, como el violín cuando las haces vibrar, su nota musical vibra a una frecuencia haciendo su ruido característico, pero hasta que la cuerda deja de vibrar emite otros sonidos a diferentes frecuencias que son los llamados Armónicos. Son estos Armónicos los que caracterizan un instrumento u otro. Hablo de instrumentos de música pero esto ocurre con todo: vibraciones de motores, voces…

Reducción del tamaño de los archivos (Compresión)
Una manera de reducir el tamaño sería quitar estos armónicos, ahorrando así en tamaño del archivo y de comprensión.
Es decir, si el audio tiene 40 sonidos y son necesarios 2 puntos para la reconstrucción de estos, tendremos que enviar 80 puntos en los paquetes de datos.
Pero si hemos calculado el espectro de la señal y observamos que únicamente para poder escucharlo necesitamos 10 sonidos ya que el resto son armónicos, necesitaremos enviar únicamente 20 puntos.
Conclusión, hemos pasado de 5 Gigas de audio a 10Kbytes
DENSIDAD ESPECTRAL
Matemáticamente lo que se hace es elevar al cuadrado, el espectro de la señal (frecuencia) tiene amplitudes a la mitad de la señal original (tiempo) por lo que al elevar al cuadrado, las amplitudes se hacen más pequeñas y desaparecen. Solo van a quedar aquellas componentes de la señal que más importantes son de la señal.
La densidad espectral lo que representa es una magnitud (dB) de cuanto de presente está esa frecuencia en la señal y si es muy importante o no para la recepción del audio, lo que vamos a escuchar.
Esto resalta las frecuencias más importantes y atenúa las menos significativas. La densidad espectral muestra cuánta energía hay en cada frecuencia y nos indica qué partes de la señal son más importantes para el audio.

